Data file: polynomial.csv
Model file: polynomial.md
Settings file: polynomial.work (automatically loads into ChaosHunter when you load the model file)
As an example of how ChaosHunter works, we build a simple set of data generated by the following polynomial:
3.2a + 4b + 5.5c^2 - 6.1d^3 + 3.3e^3
where ^ means “raised to the power of”
and a,b,c,d and e are independent variables
The idea is to see how closely ChaosHunter can approximate the polynomial.
We did not scale any inputs because we could see that they are all small numbers. We selected all Arithmetic functions, all Polynomial functions, and all but the square root and absolute value from the Algebra functions. Our goal was to maximize R-squared.
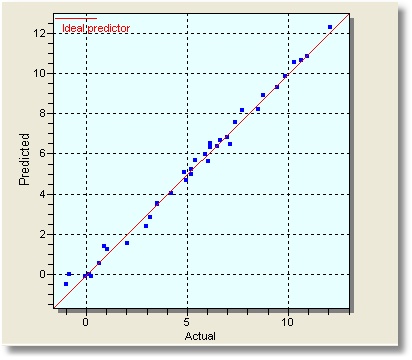
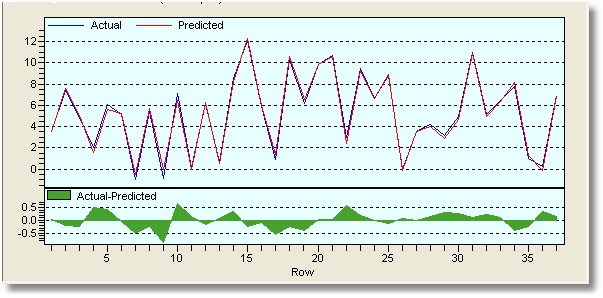
After about 1600 generations we stopped the optimization because actual vs predicted was very close, and R-squared was a little over 0.992:
. Here is the formula that was found:
Actual = (c * ((-0.1561149) * c)) + ((((-0.1561149)^2 + cube(a)^2) + 3.953567)*b+(c^2 - d^2)*5.594682+3.179821*((e)^2 + (-(-a))))
Even if simplified, this formula is not the same as the generating one, but the results are very close: